SICP 孤読書会 - 1.2 手続きとその生成するプロセス (1.2.4 〜 1.2.6)
1.2.4 べき乗
引数として底 b と正の整数の指数 n をとり、 bn を計算する手続きは再帰的な手続き、反復的な手続きで記述することができる。
再帰的な手続きでは、Θ(n)ステップ、Θ(n)スペースを必要とする。
反復的な手続きでは、Θ(n)ステップ、Θ(1)スペースを必要とする。
逐次平方を使うとより少ないステップ数でべき乗の計算をすることができる。
逐次平方では、順番に
(b * (b * (b * (b * (b * (b * (b * b))))))
を計算するのではなく
b^2 = b・b
b^4 = b^2・b^2
b^8 = b^4・b^4
を使って計算を行う。
それにより、Θ(log n)ステップ、Θ(log n)スペースでべき乗の計算をすることができる。
問題 1.16 〜 1.19
SICP/ch1/1-16.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-17.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-18.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-19.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-19.txt at master · snufkon/SICP · GitHub
github に解答をおいておく。
1.2.5 最大公約数
2つの整数a, b の最大公約数(GCD)は、a, b の両方を剰余なしに割り切る最大の整数と定義する。
GCD の計算法として Euclid のアルゴリズムがある。
Euclid のアルゴリズムを手続きとして記述すると
(define (gcd a b)
(if (= b 0)
a
(gcd b (remainder a b))))
となる。
この手続は反復的なプロセスを生成する。
問題 1.20
SICP/ch1/1-20.scm at master · snufkon/SICP · GitHub
github に解答をおいておく。
1.2.6 例: 素数性のテスト
整数 n の素数性を調べるアルゴリズムとして、2つの方法を述べる。
除数の探索
ある数(n)が素数であることは次のようにしてわかる
n は n 自身がその最小除数である時に限り、素数である。
一般的な方法。これを元に実装するとΘ(√n) のアルゴリズムになる。
Fermat テスト
素数性をテストする際に Fermat の小定理を利用する。
Fermat の小定理
n を素数、a を n より小さい正の整数とすると、a の n 乗は n を法として a と合同である。
分かりづらい。
n を素数、a を 0 < a < n の整数とすると、a^n を n で割った余りは a になる。
っていうこと。
n が素数でない時は、一般に a < n なる殆どの数について上の関係は成り立たない。
--> 言い換えると、非素数でも上の関係がなり立つ場合がある。
これらを元に実装すると、Θ(log n) のアルゴリズムになる。
除数の探索より高速であるが、確率的方法なため注意が必要。
Fermat テストで得られた答えは確率的にしか正しくない。
より正確に言うと、
n が Fermat テストに失敗 --> n は確実に素数ではない n が Fermat テストに合格 --> n が素数である可能性が非常に高い
となる。テストに合格しても n が素数であることは保証されない。
Fermat テストの実装時に必要となる expmod については
の説明が分かりやすかったです。
問題 1.21 〜 1.28
SICP/ch1/1-21.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-22.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-23.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-24.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-25.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-26.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-27.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-28.scm at master · snufkon/SICP · GitHub
github に解答をおいておく。
問題 1.23
gauche には runtime 関数がないので
実行時間の計測 - n-oohiraのSICP日記 - sicp
を参考にさせていただき、方法1で実装。
問題 1.24
fermat-test で利用している random が gauche にないため
(use srfi-27)
(random-integer n)
を利用する。
問題 1.28
何をやればいいか、いまいちピンとこなかったので
Bill the Lizard: SICP Exercise 1.28: The Miller-Rabin test
の実装を見てパクリました。
SICP 孤読書会 - 1.2 手続きとその生成するプロセス (1.2.1 〜 1.2.3)
この節では、
- 単純な手続きが生成するプロセス共通の「形」を見ていく。
- プロセスが時間とスペースという計算資源を消費する速度を調べてみる。
1.2.1 線形再帰と反復
階乗の手続きから、再帰的プロセス、反復的プロセスについて考える。
n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1
n! は (n - 1)! の結果に n をかけて計算できる。それを踏まえて
(define (factorial n)
(if (= n 1)
1
(* n (factorial (- n 1)))))
といった形で手続きを記述することができる。
この手続で6!を計算しているところを置換えモデルで記述してみる。
(factorial 6) (* 6 (factorial 5)) (* 6 (* 5 (factorial 4))) (* 6 (* 5 (* 4 (factorial 3)))) (* 6 (* 5 (* 4 (* 3 (factorial 2))))) (* 6 (* 5 (* 4 (* 3 (* 2 (factorial 1)))))) (* 6 (* 5 (* 4 (* 3 (* 2 1))))) (* 6 (* 5 (* 4 (* 3 2)))) (* 6 (* 5 (* 4 6))) (* 6 (* 5 24)) (* 6 120) 720
この形のプロセスを再帰的プロセス(recursive process)という。
再帰的プロセスの特徴
- 置換えモデルは膨張してから、収縮していく形をとる。
- プロセスを実行する際、解釈系が後に実行する演算を覚えている必要がある。
n!の計算では、ステップ数、スペース共にnに線形(比例して)成長する。
階乗の計算は別の見方で考えることができる。
n! をまず1に2を掛け、結果に3を掛け、4を掛け、nになるまで続けることで記述する。
(define (factorial n)
(fact-iter 1 1 n))
(define (fact-iter product counter max-count)
(if (> counter max-count)
product
(fact-iter (* counter product)
(+ counter 1)
max-count)))
この手続で6!を計算しているところを置換えモデルで記述してみる。
(factorial 6)
(fact-iter 1 1 6)
(fact-iter 1 2 6)
(fact-iter 2 3 6)
(fact-iter 6 4 6)
(fact-iter 24 5 6)
(fact-iter 120 6 6)
(fact-iter 720 7 6)
720
この形のプロセスを反復的プロセス(iterative process)という。
反復的プロセスの特徴
- 置換えモデルは伸び縮みしない。
- どの時点においても、プログラム変数がプロセスの状態の完全な記述を持っている。
n!の計算では、ステップ数はnに線形(比例して)成長するものの、スペースは固定値となる。
問題 1.9, 1.10
SICP/ch1/1-9.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-10.scm at master · snufkon/SICP · GitHub
github に解答を追加。
問題1.10 は置換えモデルをノートの書きながら考えた。
1.2.2 木構造再帰
計算でよくあるパターンとして、木構造再帰(tree recursion)がある。
Fibonacci 数を再帰的手続きで
(define (fib n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (fib (- n 1))
(fib (- n 2))))))
木構造再帰プロセスは効率は良くないが、プログラムの理解や設計を支援してくれる。
問題 1.11 〜 1.13
SICP/ch1/1-11.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-12.scm at master · snufkon/SICP · GitHub
SICP/ch1/1-13.txt at master · snufkon/SICP · GitHub
に解答を追加。
問題1.13 は他の方の答えをチラ見してから自分で解いてみた。
証明問題は苦手。
2.2.3 増加の程度
オーダーも苦手意識がある。
なんというか、だいたいな感じがしっくりこない。(オーダーの定義自体がそういうものだけど)
計算の資源を消費する速度は、プロセスによって大きく異なる。
増加の程度(order of growth)の考えを使うことにより、プロセスが必要とする資源を粗く見積もることができる。
n : 問題の大きさを表すパラメタ
R(n): 大きさ n の問題に対してプロセスが必要とする資源の量を表すパラメタ
とする。
十分大きな n の値に対し、
k1 * f(n) <= R(n) <= k2 * f(n)
となる n と独立な正の定数, k1, k2 があるとき
Θ(f(n)) を R(n) の増加の程度という。
増加の程度はプロセスの振舞いを大まかに記述したもの。
そのため、
- n2 のステップが必要なプロセス
- 1000 * n2 のステップが必要なプロセス
- 3 * n2 + 10 * n + 17 のステップが必要なプロセス
は全てΘ(n2) になる。
問題 1.14
SICP/ch1/1-14.png at master · snufkon/SICP · GitHub
SICP/ch1/1-14.scm at master · snufkon/SICP · GitHub
に解答を追加。
木構造を描く方は問題ない。がスペースとステップ数の増加に程度は解答に辿りつけず、、、
他の方の解答を見させてもらいました。
Bill the Lizard: SICP Exercise 1.14: Counting change
英語ですが、ここが一番分かりやすかった。
この問題、解答はなんとなく分かっても自信がないと言っている人(web上で)が多い気がします。
計算量の問題はみんな苦手なんですかね。自分もかなり苦手です。
のちのちのため、英語ページの解答を追っておきます。(図をお借りします)
スペース
両替の金額の増加につれ、プロセスが使うスペースの増加の程度を求める問題。
こっちは、英語の解答が詳しくないため自分で考える。

図をちょっとお借りする。
(count-change 11) の計算は再帰的に行われる。
図の (cc 11 4) の計算をしている際には、
(count-change 11)
↓
(cc 11 5)
↓
(cc 11 4)
の流れで計算が実行されており、プログラム全体としてはこの流れで計算していることを覚えておく必要がある。
同様に (cc 11 3) の計算では
(count-change 11)
↓
(cc 11 5)
↓
(cc 11 4)
↓
(cc 11 3)
の流れをプログラム全体として覚えておく必要がある。
この覚えているのに必要な資源(メモリ, ディスクなど)がスペースにあたる。
count-change のプログラムを実行している際、一番スペースが必要な計算は図の左下の計算をしているときになる。
count-change で計算する金額が12, 13 ... と増えていくと構成図の左下ノード数は比例して1つずつ増えていく。
よって、count-change での両替の金額を n とすると、プロセスが使うスペースのオーダーは
O(n)
となる。
ステップ数
両替の金額の増加につれ、プロセスが使うステップ数の増加の程度を求める問題。
ひとまず、両替に使用するコインの数を1(1セント硬貨)として考える。
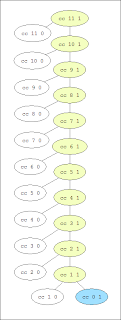
11セントの両替プロセスを描いたグラフに、コインを1枚利用した場合の木構造が現れているのでこの図を元に考える。
関数 T(n, k) を定義しておく。
T(n, k) は (cc n k) によって生成される cc の数を表す。
n, k はそれぞれ、両替の金額、両替に使用するコインの数を表す。
T(1, 1) は 図の (cc 1 1) 以下にあるノードの数から 3。 T(2, 1) は 図の (cc 2 1) 以下にあるノードの数から 5。
一般化すると
T(n, 1) = 2n + 1
となる。
オーダーで表すと、無視できる項、係数が取り除かれ
O(n)
になる。
これは、コインの数が1枚の場合のステップ数の増加の程度を表す。
次にコインの数が2枚(1セント、5セント)の場合を、(cc 50 2) のグラフから考える。
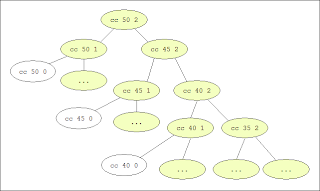
この図から2つのことがわかる。
- 2つのコインを使う場合(k = 2)の cc は n/5 回実行される。(図の右側の斜め部分)
- n/5 回実行される (cc n 2) はそれぞれ、(cc n 1) を部分木として持つ。
これらから、
T(n, 2) = (n/5) * T(n, 1) = (n/5) * (2n + 1)
オーダーで表すと、無視できる項、係数が取り除かれ
O(n2)
となる。
同じように、コインの数が3枚(1, 5, 10セント)の場合を、(cc 50 3) のグラフから考える。

T(n, 3) = (n/10) * T(n, 2)
オーダーで表すと
O(n3)
になる。
コインの数が4, 5枚になった際も同じパターンになることが明らかなため、
T(n, 5) の場合のオーダーは O(n5)。
両替の金額の増加につれて必要なステップ数の増加の程度は、
O(n5)
となる。
最初、使用するコインの影響で計算量はかなり変わって来るのでは?と思っていました。 が、計算過程でわかるように、使用するコインの数が増えたり、コインの金額が変化しても オーダーとして計算量をざっくりと表す場合には影響しないことがわかりました。
問題 1.5
SICP/ch1/1-15.scm at master · snufkon/SICP · GitHub
に解答を追加。
問題1.4に比べれば簡単。
a / 3^x < 0.1
を満たすxのうち最小の整数(x>=0)が sine の計算時に手続き p を作用させる回数になる。
式を変形すると
10a < 3^x log10a < x (logの底は3) x > log10a
となる。
よって、ステップ数のオーダーは、O(log a)となる。
必要なスペースはステップ数に比例するので、オーダーは同じく O (log a)になる。




